info@gerb.com
高層ビル向け減衰技術に関するケーススタディ:快適性と安全性
高層ビル・都市居住協議会(CTBUH)制振システムガイドライン
ティッセンクルップの試験塔、ロットヴァイル/ドイツ
プロジェクトデータ
- 完成年:
2016年(最高点到達) - デベロッパー/建設業者/所有者:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - 建築物設計者:
Werner Sobek with JAHN Architects(シュツットガルト/シカゴ) - 構造設計者:
Werner Sobek(シュツットガルト) - ダンパーサプライヤー:
GERB Vibration Control Systems - 試験ラボ:
Wacker Ingenieure (風力エンジニアリング / 風洞試験) - 高さ / 階高:
246 m / 3.3 m (オフィススペース) - 細長比:
1/11.8 - 階数:
27階 / 8階分はオフィススペース - 塔の総専有面積
340 ㎡ - 建物の機能:
エレベーター試験塔/オフィス/展望台(232 m) - 構造材:
鉄筋コンクリート(C50/60) / 鉄骨構造上のPTFEメンブレンファサード - 構造システム:
いかだ基礎上のカンチレバー型鉄筋コンクリートコア
(-32 m) - 採用された制振戦略:
ハイブリッド型マスダンパーシステム(240 t)

1.0 紹介/沿革
エレベーター技術におけるイノベーション用試験施設を収容する目的で、ドイツ南西部に高さ246 mの塔が建てられました。塔は直径20 mの円形のフットプリントの上に建っており、9 つの試験用エレベータシャフト、消防用エレベータ、ガラス製パノラマビューエレベータ用にスペースを提供しています。さらに、試験プログラムを補助する目的で、220 mのシャフトが機械的リフティング用シャフトとして使用されています。
直径40 mの塔の基礎部分にはサービス施設、ロビー、教育センター用の追加スペースが提供されています。232 mのドイツで最も高い展望台からは、晴れた日にはシュヴァルツヴァルト、さらにはアルプスの壮大な景色を眺めることができます。

2.0 構造システム
試験塔の構造システムは、基本的に直径20.8 mの鉄筋コンクリート管となっており、30 mの深さまで周囲の土によって支えられています(図2を参照)。管の厚さは110 mの高さまでは40 cm、それ以上は25 cmとなっています。コイパー層とその下のシェル石灰石からなる土壌は、高い支持力を提供しているため、杭基礎は必要ありませんでした。周囲の土によるクランプ効果に加え、塔の基礎のより広い構造が、より高い横方向の剛性を提供します。
コンクリート管内部の剛性は、主にエレベータシャフトの内壁によるものです。エレベーターシャフトへは、天井スラブが事前に設置されている特定の高さレベルでのみアクセスできます。エレベーターシャフトのいくつかは115 mの高さまでとなっており、鋳造された厚さ40 cmの長いフロアで所定の位置に固定されています。これらのフロアはオフィススペースとして使用されます。高さ197 mまでのボイドスペースの上は、蓄熱およびTMDシステムに使用されます。塔の最上部は、オフィススペースと残りのエレベーターシャフトに使用されます。

試験塔の特徴としては、PTFEコーティングを施したガラスファイバーメッシュによるテキスタイルファサードです。メッシュの開口幅は、建物の高さとともに増加し、ファサードは徐々に半透明性が高くなり、材料の密度と重量を低減し、空力効果を向上させています。
ファサードのらせん形状は、スクルートンらせんとして機能することを想定しており、ファブリック自体がコンクリート構造に陰を提供し、直射日光の熱による応力発生を回避するのに役立ちます。ファサードの設計、そして設置における材料面の選択については、メンテナンス性と耐久性、および風荷重を考慮する必要がありました。
3.0 建設工法

試験塔の建設は、以下の手順で行われました。
- 塔の基礎用として30 mの円形建設ピットの掘削。掘削と成形は、まず爆破によって行われました。掘削後、ピットはグラウンドアンカーとコンクリートの吹き付けによって固定されました。
- いかだ基礎の注入
- スリップフォーミングを使用した垂直方向のコンクリート構造物の建設。すべての壁には、4か月間継続して建設が行われました
- フロアスラブの建設
- エントランスエリアの建設
4.0 風荷重に対して予測される動的応答
試験塔の基本振動数は、建設段階とコンクリートの状態(ひび割れ/ひび割れなし)に応じて、0.17 Hz 〜 0.20 Hzの範囲であると予測されました。図4を参照
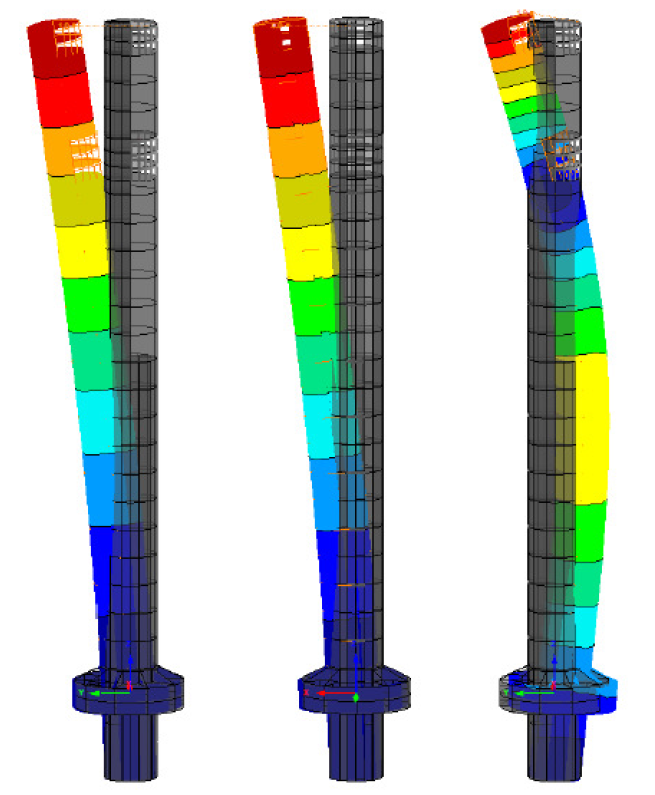
風解析より、構造物の渦励振は、風速15.3〜16.7 m/s(高さ10m)の範囲において発生しうることが明らかになりました。減衰機能の追加がなければ、この渦励振は上部構造で約+/- 750 mmの振動を引き起こし、内部の職員に不快感を与えるだけでなく、塔のコンクリート構造に重大な疲労寿命への影響を引き起こすと予想されました(図5を参照)。横風による渦励振に対する動的応答を低減するため、パッシブ型チューンドマスダンパーが設置されました。
塔は揺れに敏感なエレベータ設備を構築するための試験塔として使用されるため、所有者は、穏やかな日に塔を強制的に振動させる機能を持ちつつ、 疲労の問題を引き起こさないソリューションを探しておられました。強制的な揺れに要求される振幅レベルは、約+/- 200mmの安全な範囲が設定されました。この要件は、ハイブリッドマスダンパー(HMD)または、設計システムは過去に導入された他のHMDシステムとは異なるため、いわゆるデュアルユースTMDを実装するまれな機会を提供しました。このシステムは、パッシブシステムの最適化、アクチュエータのメカニズムの設計、制御アルゴリズム、および安全コンセプトを含め、以下の章で説明します。

5.0 パッシブ型チューンドマスダンパーシステムの最適化
パッシブ型TMDシステムのパラメータは、3つの異なる側面を考慮して特定する必要がありました。つまり、a)追加で十分な構造的減衰機能を提供し、渦励振による動的応答を低減すること、b)パッシブモードで結果として生じるTMD主質量の移動を制限し、横風の突風による励振下にある場合は実現可能/実際的な値とすること、そして c)提供されたアクチュエータによる性能エンベロープを考慮し、励振モードでの望ましい塔の最大変位に必要なエネルギー入力に基づきTMD質量体を選択することです
(つまり、稼働中に発生する最大の力と最大ストローク)。TMDシステムを最適化するために、塔の質量分布、および特定された構造特性で報告されている質量慣性モーメントを表す数値モデルが使用されました。フロア間の剛性要素も、モード形状と実物スケールでの観察からの固有振動数に一致するように調整されました。図6 – 左の図は、採用された類似モデルのモード形状と固有振動数を示しています。図6 – 左の図では、類似モデルのモード形状を、構造コンサルタントが作成した詳細モデルのものと比較しています。
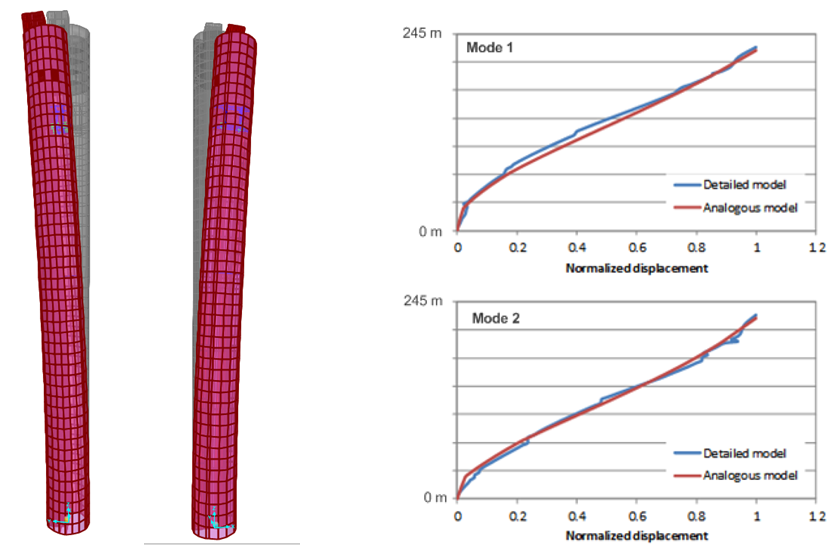
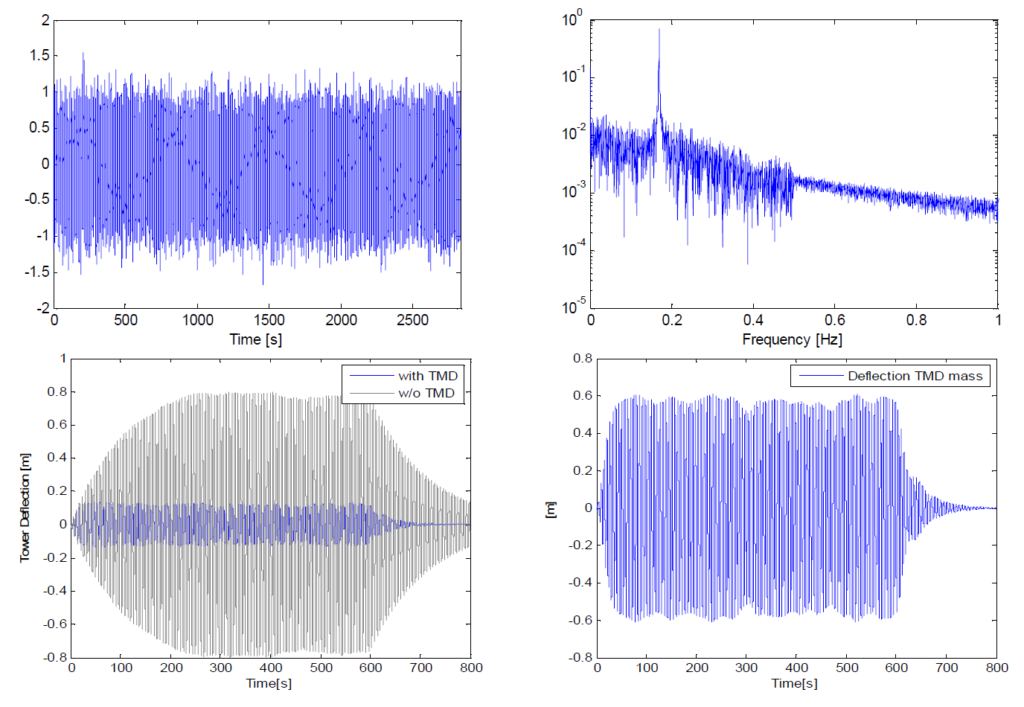
また、TMDは、塔での変位位置もキャプチャする振り子システムとして個別にモデル化されています。支配的な入力ケースの負荷特性、つまり渦励振による共振振動は、単一正弦波振動のそれと非常に類似しています。それでも、共存する風荷重は、本質的に確率的性質のものであり、そのためには、よく知られたDen Hartog条件以外の最適化条件が適用されます。さらに、TMD質量体の相対変位は、調和型荷重よりも確率的荷重に対しての方が大きくなります。最適なTMDパラメータ値の特定には、実際の荷重に近いものを考慮する必要があるため、確率的風荷重(Davenportスペクトルに基づく)と、(渦励振のような)全体的な横風励振に代表される重ね合わせた共鳴コンポーネントの両方を含む時間履歴が生成されました(図7-右を参照)。最適化されたパッシブ型TMDシステムで実現できる塔の変位低減と、その結果生じるTMDの変位を図7-右に示します。
ξ=0.8 %の推定構造減衰に関するこれらの結果に基づき、変位を+/- 650 mm以内に維持しつつ、最適なTMD減衰率を維持し、最高のTMD性能を実現するには、240 tのTMD質量体が必要であることがわかりました。TMD減衰の増加は変位を抑制する可能性があるが、これはアクチュエータの力要件に悪影響を及ぼします。最適化された240 tのTMDセットアップに必要な力を特定するため、類似のモデルを使用して、アクチュエータからの最大力40 kNで、塔の変位が+/- 200mmの範囲となることを確認しました。図7は、類似の数値モデルにおける時間ドメイン数値シミュレーションの結果を示します。このために、結果として生じる塔最上部の変位、TMD質量体の変位、およびそれらを引き起こす有効な力が表示されます。


6.0 制御システムの説明
制御システムの二重性は、a)通常のパッシブモードで発生する振動を低減してエネルギー消費の削減に役立ち、b)共振効果を利用してメインのTMD質量体を励振し、最終的に実際の力の需要を満たすことにより、アクチュエータに求められる力を低減します。したがって、他の制御システム(図10を参照)と比較して、アクチュエータは主要構造物とTMD質量体を接続しますが、典型的なアクティブマスドライバー/ダンパーシステムの場合のようにTMD質量体を直接制御するためには使用されません。
実装されたデュアルユースTMDには、パッシブモード用の240 tの応答質量体が選択されました。励振モードでは、2つのリニアドライブ(各方向に1つずつ)がTMD質量体に取り付けられ、ねじれによるアーチファクトを回避するために、質量体の重心近くにピボットがあります。 各リニアドライブは、+/- 600 mmの最大ストローク内で最大40 kNの力を提供できます(詳細は図9を参照)。リニアドライブは取り外し可能であるため、万が一ベアリングが故障した場合でも、パッシブモード全体がアクチュエータのベアリングの影響を受けることはありません。
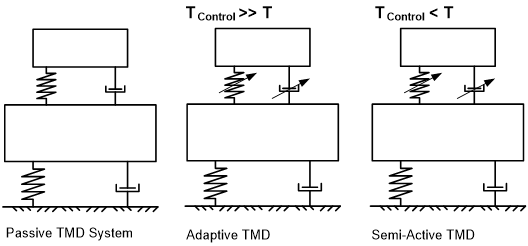
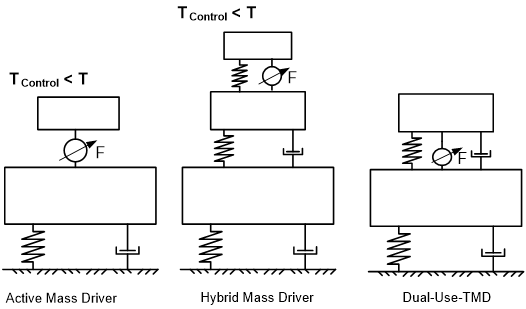
図10 – 制御システムのタイプ – パッシブ、セミアクティブ、アクティブ、およびハイブリッドシステムと比較におけるデュアルユースTMD
このシステムには、塔の最上部レベルとTMDの質量加速度を計測するために、4つの加速度計(各方向に1つ)が装備されています。加速度信号は、塔の基本固有振動数(0.1〜0.3 Hz)の範囲内でバンドパスフィルター処理され、塔の速度と変位を特定するために積分されます。
さらに、積分された変位値は、信号のドリフトを比較するために最上部にも設置されている付属のグローバルナビゲーション衛星システムの値と比較できます。初期相関テストは、それに応じて実行されました。加えて、TMDの変位は、リニアモーター内に統合されたストリングポットトランスデューサと誘導長測定システムで直接監視されます。
7.0 制御アルゴリズム
塔の一般的な制御ループは図11にあり、これは、閉ループ制御シーケンスを示しています。制御アルゴリズムの詳細な設計には、アクチュエータとTMD質量体の相互作用に基づく分析モデルが必要で、それにより、アクチュエータ入力と加えられた作用力との間の関係が特定されます。これらは、建物全体の動的挙動を説明する主要構造の分析モデルと組み合わせる必要があります。さらに、 [2]や[3] のように、他のHMDアプリケーションに適用された、または [1] のように理論的に調査された標準制御アルゴリズムと比較して、この塔アプリケーションの制御アルゴリズムでは、1つの主方向の同期制御励振と垂直方向の振動低減を考慮する必要がありました。
基本モードで主に動的応答が期待されるため、不安定性を回避するためのすべてのメリットを備えたリニアフィードバック制御をこれらの両方のタスクに適用できます。実際に行われているシンプルな制御として、励振に垂直な塔の動的応答を減衰させるリニアフィードバック制御は、7つの構造動的測定の指定された加重線形合計を通じて該当するアクチュエータを駆動します。これらの測定は、TMDと塔の最上部の加速度、TMDと塔の最上部の速度、TMDと塔の最上部の変位、およびTMDの塔の最上部に対する相対変位に対して行われます。
ここで、事前に選択された重み係数は、単純、正または負のスカラーゲインであることに注意が必要です。重み係数のパラメータ化は、塔の動的試験に基づいており、振動数依存の変更は行われません。アクチュエータの有効なフィードバックは瞬時に(50Hz)計算され、これも以前の動的測定の線形結合となっています。非線形の操作は行われません。制御設計は、アクチュエータ制御における振動低減性能を証明するために、時間ドメインの数値シミュレーション(つまり直接積分)でも実施されました。励振モードでは、同じ制御アプローチが、目的の変位値への塔の励振を表す変位オフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、その他の外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、それに応じて制御値が調整されます。
励振方向に垂直な塔の動的応答を低減するための線形フィードバック制御により、アクチュエータへの力コマンドを、プログラムの7つの動的測定値の指定された加重線形和にできます。これら7つの測定は、TMDと塔の加速度、TMDと塔の速度、TMDと塔の変位、およびTMDの塔に対する相対変位。ここで、重み係数は、単純、正または負のスカラー値であることに注意が必要です。重み係数のパラメータ化は、塔の実験的な動的試験に基づいて行われます。有効なアクチュエータフィードバックは瞬時に(50Hz)に計算され、
重み係数はスカラー量であり、振動数依存の伝達関数の形式を使用していません。また、フィードバックは動的特性の線形結合です。非線形の操作やロジックはありません。制御設計は、時間ドメインの数値シミュレーション(直接積分)のために実装され、各時間ステップで、アクチュエータ制御としてのTMD質量体への力入力を適合させることができました。図12は、振動抑制のシミュレーションの結果、つまり塔の変位そしてその結果として生じるTMD質量体の変位を示しています。
励振モードでは、同じ制御アプローチが、塔の励振を目的の変位値に表すオフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、
それに応じて制御値が調整されます。このオフセットでは、重み係数が実験により特定されました。図13は、単純な正弦波励振と制御アルゴリズムを適用した励振モードでの突風荷重外乱の数値結果を示しています。
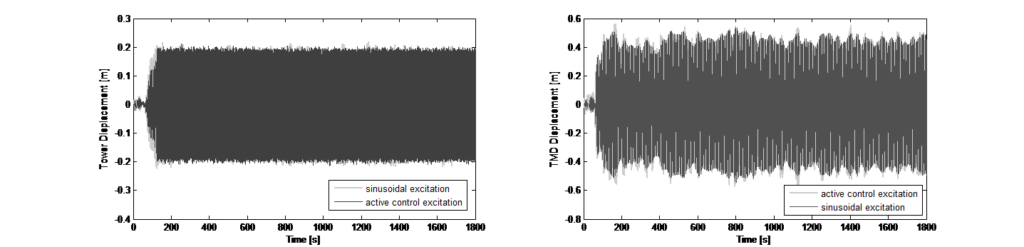
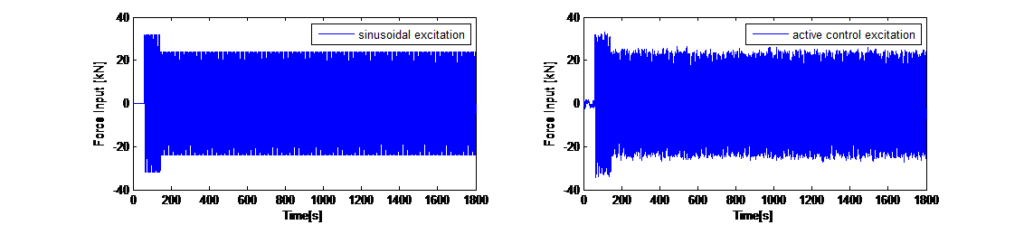
8.0 安全性コンセプト
アクチュエータとして使用されるリニアドライブで提供可能な+/- 40 kNの力を考慮し、塔の変位が疲労規定を超えないようにするための安全コンセプトが必ず必要です。これは、力の出力が、所定の+/- 200mmを超える最上部の変位を引き起こすのに十分でない場合にも適用されます。システムの安全性を高めるためのアプローチの1つは、塔の最上部の変位を記録している監視センサーの冗長性を高めることでした。これには、現在の制御ハードウェアとは異なる測定原理を最適に使用する追加の独立した監視システムを実装するのが一番です。ここで紹介されたプロジェクトでは、引用されているように、制御ハードウェアが加速度計、そして構造物の固有振動数の範囲内で信号バンドパスフィルタリングに対して定義された加速度閾値を使用しました。最優先される上位監視システムは、精度が+/- 10 mmのグローバルナビゲーション衛星システム(GNSS)です。
GNNSシステムには、座標データを実際の変位応答値に変換する参照基地局が必要となります。人工励振モード中に塔の最上部変位が所定の閾値を超えると、追加の風やその他の励振が原因となる可能性があり、リレーがアテンダンス信号を0Vに切り替えます。これにより、人工励振モードが中止されます。さらに、両監視システムは、取得したデータに障害のあるセンサー信号がないか常に確認するため、励振モードが有効な場合は中止されます。誤った加速度/ストリングポット信号は、スペクトルピークピッキング条件によって検出されます。該当する範囲でのピークピッキングが可能な場合にのみ、センサーが正しい信号を提供していると見なすことができます。GNNSシステムは、座標データの変化を分析しますが、サンプリングされたデータが時間とともに変化しない場合は、信号における障害が自動的に想定されます。
9.0 振動試験
塔の初期振動試験は、塔がまだ完成していない段階で実施されたため、この段階でのタワーの基本振動数は、パッシブ型TMDシステムが指定した調整範囲を上回っています。TMDは、可能な限り高いチューニング周波数に調整されています。振動試験の目的は、TMDシステムがブロックされた状態で、塔の基本振動数と固有の構造減衰を特定することでした。さらに、パッシブ型TMDシステムを使用した場合の動的挙動と、パッシブ型TMDシステムによる構造的な減衰の増加を特定する必要があります。塔の基本固有振動数を特定するには、平均正規化出力スペクトル密度(ANPSD)法 [1] を利用できます。このためには、記録された時間履歴をセグメントに分割する必要があります。これらのセグメントを周波数ドメインに変換する必要があります。結果として得られるスペクトルは、正規化、平均化し、複素共役スペクトルとの乗算を行う必要があります。
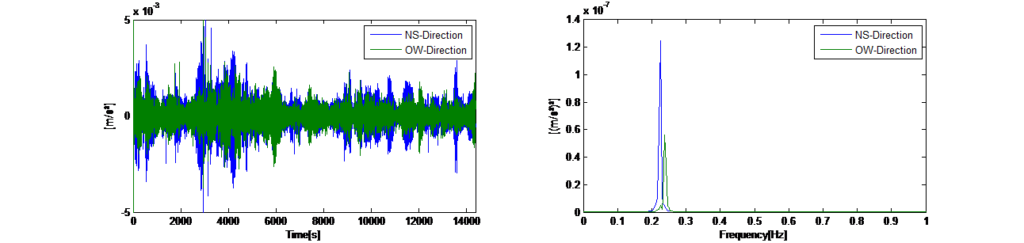
これにより、あらゆるランダムな振動が排除され、構造物で繰り返し発生する自由振動のみが平均化されたスペクトルに表示されます。これは、塔の主に励起された固有振動数を表します。図14の左は、TMDがロックされた状態でのx方向とy方向の水平周囲振動に関して記録された時間履歴を示します。図14の右は、120 秒のセグメント長における平均自動出力スペクトルを示しています。スペクトルは、塔が2つの主要な振動数(x方向に0.225 Hz、y方向に0.245 Hz)で動的応答を示すことを意味しています。
対象の振動モードにおいて周囲の励振が十分な動的応答を引き起こし、確率論的確実を得ると想定している上記の平均出力スペクトル法に加え、固有振動数は、強化型周波数ドメイン分解機能と確率的部分空間同定法を組み込んだ、 [1] 市販の信号処理ソフトウェアARTEMISを使用して特定されました。
強化型周波数ドメイン分解機能(EFDD)と確率的部分空間同定法は、出力のみのモーダルパラメータの特定同定に広く使用されています。
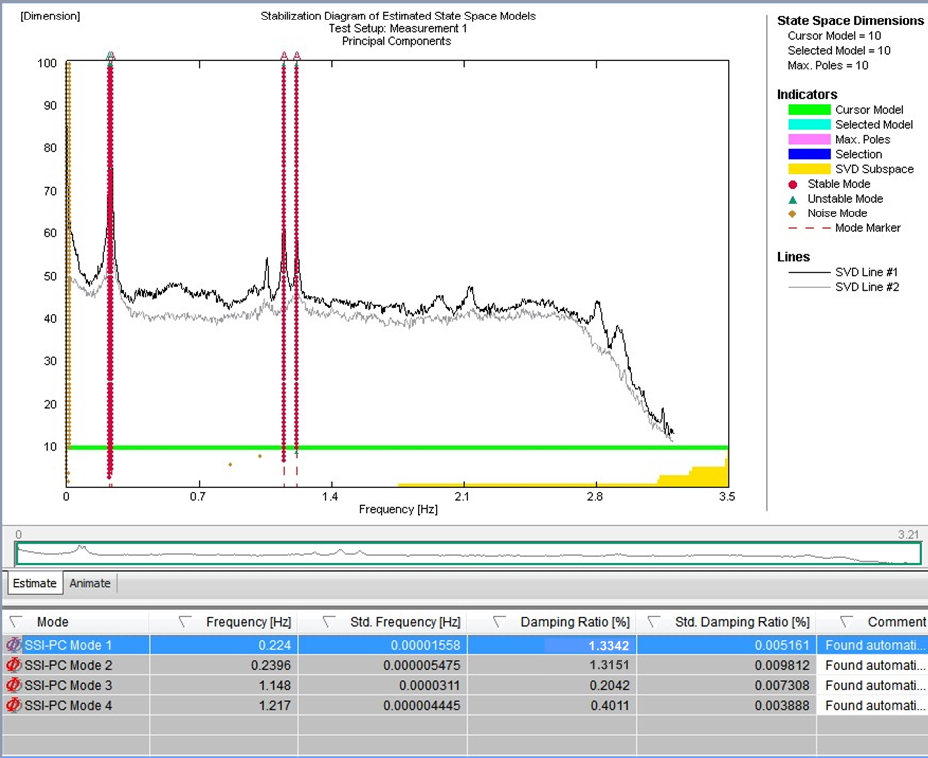
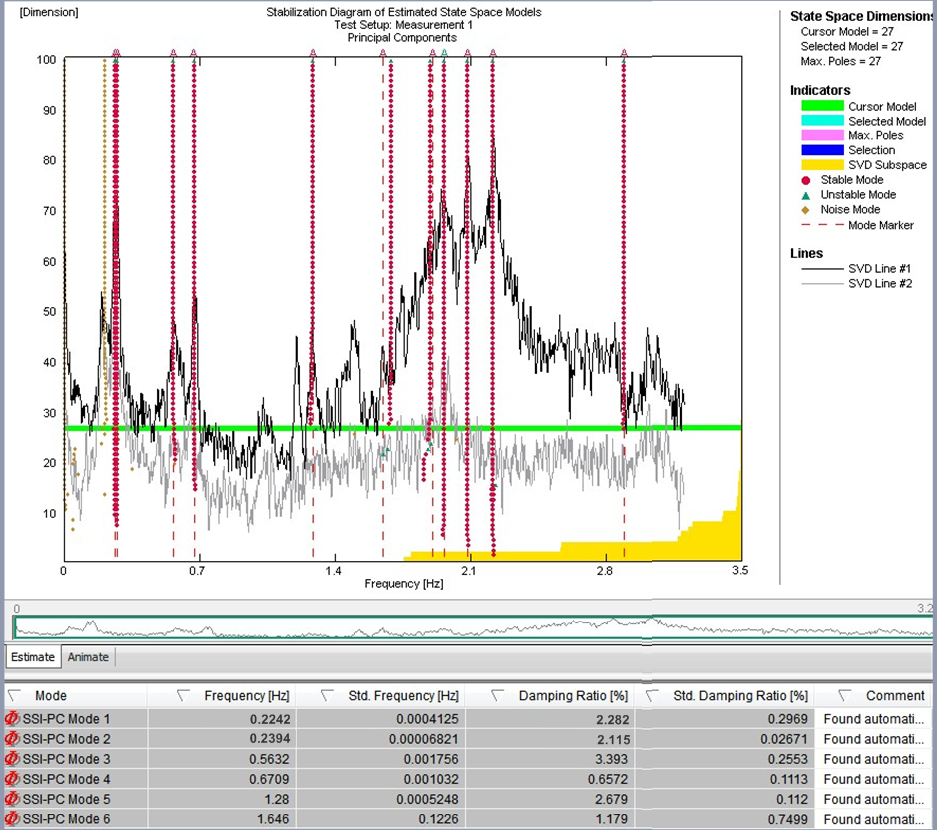
図15 – TMDがブロックされた状態(左)と TMDが有効化された状態(右)での周囲振動記録の安定性カード
EFDD法は、応答スペクトルの計算に依存します。したがって、スペクトル推定の誤差を低いレベルに保ち、信頼できる方法でモーダルパラメータを抽出するには、長い記録が必要となります。確率的部分空間同定アルゴリズムは、出力のみのモデルを使用してブリッジを特定するために適用されました。確率的部分空間同定法は時間ドメインで機能し、動的問題の状態空間記述に基づいています。異なるモデル次数でのシステム同定結果を比較し、いわゆる安定化図で真の構造モードとスプリアスモードから区別します。これらの図は、特定されたシステムモデルを選択するために広く使用される方法で、真の構造モードが連続するモデル次数に対して安定している傾向があり、自動化された手順で評価される特定の安定化条件を満たしています。図15は、記録された周囲データの安定性カードを示しており、このカードから、該当するモードを特定できます。特定されたモードと、TMDがロックされた状態(左)とTMDが有効な状態(右)での各モードの特定された減衰率も図14に示されています。これにより、構造的な減衰の増加に気付くことができます。構造的な減衰の増加は、調整されていないTMDセットアップが考慮された理論モデルから特定できる理論値の範囲内にあります。
パッシブ型TMDシステムを使用した周囲振動試験に加え、調整されていないTMDシステムの状態にもかかわらず、アクティブ励振モードによる予備テストが行われました。図12の左は、塔の最上部で記録された加速度の時間履歴を示しています。最初の正弦波励振の後、安定した加速レベルのアルゴリズムを有効にして、塔の変位とTMD質量体の強制変位との相関関係を実験で特定しました。図14に示された時間履歴は、励振モードでの2つのテストシナリオを示し、対応するFFTスペクトルは、2つの基本振動数(x方向とy方向)での塔の明確な応答を示しています。 緑でマークされた時間セクションは、アクティブ制御が無効になっている質量体の正弦波励振であり、両方の主方向に動的応答が引き起こされています。結果としてのFFTスペクトルは、2つのピークを示し、これら2つの方向の基本振動数を特定できます。青でマークされた時間セグメントは、アクティブ制御が有効になっている励振用であり、主に一方向でより安定した塔の変位が引き起こされています。励振モードがオフに切り替えられた後に生じる振動の減衰も、構造的減衰を特定するために使用され、D=2.4 %との結果になりました。この結果は、SSIアルゴリズムで特定された減衰率と相関しています。
10.0 結論と展望
デュアルユースTMDは、基本振動数で制御された動的応答に塔を意図的に励振することを目的として、高さ246 mのティッセンクルップ試験塔に設置されています。この励振の目的は、塔の2つの主要な方向に、定義された建物の揺れを引き起こすことです。数値計算に基づき、パッシブモードで必要な減衰により、+/- 200 mmの塔の最上部の変位を実現するために必要な制御力には240 tのTMD質量体が必要であることがわかりました。励振モードの安定した変位レベルを実現し、風と垂直方向の強制振動成分によって引き起こされる変位を抑制するために、制御アルゴリズムが開発され、数値シミュレーションでのテストが行われました。コンクリートスラブを質量体として使用したパッシブ振り子型TMDシステムを設置した後、アクチュエータを稼働させ、初期試験を実施しました。テストにより、塔の固有の構造減衰が予想よりも高いことが明らかになり、関連するすべてのモードを明確に特定できました。建物のアクティブ励振モードは機能しており、建物がまだ完成していないため、すべての動作パラメータを導出するために完全ではないものの、テストは実施できます。建物がまだ完成していない状態であるため、パッシブ型TMDを特定された基本振動数に適合させることはできませんでした。
TMDシステムの適応が完了すれば、すぐにでも引き続きテストを実行できます。これには、振幅依存の減衰と安全コンセプトの完全性に関するテストも含まれます。
参考資料
[1] Wenzel, H., Pichler, D., Schedler, R.(1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.:Mevel, L. (2012).“Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000).“Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003).Passive and active mass damper control of the response of tall buildings to wind gustiness.Eng.Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings.J. Eng.Mech.2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building.Earthq.Eng.Struct.Dyn.2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower.CTBUH J. 2012, 24–29.
[8] Soong, T.T.“Active Structural Control:Theory and Practice”; John Wiley & Sons, Inc.:New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
その他の情報源
このトピックに関する詳細な情報が必要ですか?
ご不明な点は、お気軽にお問い合わせください。
当社のプロジェクトエンジニアがまもなくご連絡させていただきます。
高層ビル向け減衰技術に関するケーススタディ:快適性と安全性
高層ビル・都市居住協議会(CTBUH)制振システムガイドライン
ティッセンクルップの試験塔、ロットヴァイル/ドイツ
プロジェクトデータ
- 完成年:
2016年(最高点到達) - デベロッパー/建設業者/所有者:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - 建築物設計者:
Werner Sobek with JAHN Architects(シュツットガルト/シカゴ) - 構造設計者:
Werner Sobek(シュツットガルト) - ダンパーサプライヤー:
GERB Vibration Control Systems - 試験ラボ:
Wacker Ingenieure (風力エンジニアリング / 風洞試験) - 高さ / 階高:
246 m / 3.3 m (オフィススペース) - 階数:
27階 / 8階分はオフィススペース - 塔の総専有面積
340 ㎡ - 建物の機能:
エレベーター試験塔/オフィス/展望台(232 m) - 採用された制振戦略:
ハイブリッド型マスダンパーシステム(240 t)

- 構造材:
鉄筋コンクリート(C50/60) / 鉄骨構造上のPTFEメンブレンファサード - 構造システム:
いかだ基礎上のカンチレバー型鉄筋コンクリートコア
(-32 m)
高層ビル向け減衰技術に関するケーススタディ:快適性と安全性
高層ビル・都市居住協議会(CTBUH)制振システムガイドライン
ティッセンクルップの試験塔、ロットヴァイル/ドイツ
プロジェクトデータ
- 完成年:2016年(最高点到達)
- デベロッパー/建設業者/所有者:Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators
- 建築物設計者:Werner Sobek with JAHN Architects(シュツットガルト/シカゴ)
- 構造設計者:Werner Sobek(シュツットガルト)
- ダンパーサプライヤー:GERB Vibration Control Systems
- 試験ラボ:Wacker Ingenieure (風力エンジニアリング / 風洞試験)
- 高さ / 階高:246 m / 3.3 m (オフィススペース)
- 階数:27階 / 8階分はオフィススペース
- 塔の総専有面積340 ㎡
- 建物の機能:エレベーター試験塔/オフィス/展望台(232 m)
- 構造材:鉄筋コンクリート(C50/60) / 鉄骨構造上のPTFEメンブレンファサード
- 構造システム:いかだ基礎上のカンチレバー型鉄筋コンクリートコア (- 32 m)
- 採用された制振戦略:ハイブリッド型マスダンパーシステム(240 t)

1.0 紹介/沿革
エレベーター技術におけるイノベーション用試験施設を収容する目的で、ドイツ南西部に高さ246 mの塔が建てられました。塔は直径20 mの円形のフットプリントの上に建っており、9 つの試験用エレベータシャフト、消防用エレベータ、ガラス製パノラマビューエレベータ用にスペースを提供しています。さらに、試験プログラムを補助する目的で、220 mのシャフトが機械的リフティング用シャフトとして使用されています。
直径40 mの塔の基礎部分にはサービス施設、ロビー、教育センター用の追加スペースが提供されています。232 mのドイツで最も高い展望台からは、晴れた日にはシュヴァルツヴァルト、さらにはアルプスの壮大な景色を眺めることができます。

2.0 構造システム
試験塔の構造システムは、基本的に直径20.8 mの鉄筋コンクリート管となっており、30 mの深さまで周囲の土によって支えられています(図2を参照)。管の厚さは110 mの高さまでは40 cm、それ以上は25 cmとなっています。コイパー層とその下のシェル石灰石からなる土壌は、高い支持力を提供しているため、杭基礎は必要ありませんでした。周囲の土によるクランプ効果に加え、塔の基礎のより広い構造が、より高い横方向の剛性を提供します。コンクリート管内部の剛性は、主にエレベータシャフトの内壁によるものです。
エレベーターシャフトへは、天井スラブが事前に設置されている特定の高さレベルでのみアクセスできます。エレベーターシャフトのいくつかは115 mの高さまでとなっており、鋳造された厚さ40 cmの長いフロアで所定の位置に固定されています。これらのフロアはオフィススペースとして使用されます。高さ197 mまでのボイドスペースの上は、蓄熱およびTMDシステムに使用されます。塔の最上部は、オフィススペースと残りのエレベーターシャフトに使用されます。試験塔の特徴としては、PTFEコーティングを施したガラスファイバーメッシュによるテキスタイルファサードです。メッシュの開口幅は、建物の高さとともに増加し、ファサードは徐々に半透明性が高くなり、材料の密度と重量を低減し、空力効果を向上させています。

ファサードのらせん形状は、スクルートンらせんとして機能することを想定しており、ファブリック自体がコンクリート構造に陰を提供し、直射日光の熱による応力発生を回避するのに役立ちます。
ファサードの設計、そして設置における材料面の選択については、メンテナンス性と耐久性、および風荷重を考慮する必要がありました。
3.0 建設工法

試験塔の建設は、以下の手順で行われました。
- 塔の基礎用として30 mの円形建設ピットの掘削。掘削と成形は、まず爆破によって行われました。掘削後、ピットはグラウンドアンカーとコンクリートの吹き付けによって固定されました。
- いかだ基礎の注入
- スリップフォーミングを使用した垂直方向のコンクリート構造物の建設。すべての壁には、4か月間継続して建設が行われました
- フロアスラブの建設
- エントランスエリアの建設
4.0 風荷重に対して予測される動的応答
試験塔の基本振動数は、建設段階とコンクリートの状態(ひび割れ/ひび割れなし)に応じて、0.17 Hz 〜 0.20 Hzの範囲であると予測されました。図4を参照

風解析より、構造物の渦励振は、風速15.3〜16.7 m/s(高さ10m)の範囲において発生しうることが明らかになりました。減衰機能の追加がなければ、この渦励振は上部構造で約+/- 750 mmの振動を引き起こし、内部の職員に不快感を与えるだけでなく、塔のコンクリート構造に重大な疲労寿命への影響を引き起こすと予想されました(図5を参照)。横風による渦励振に対する動的応答を低減するため、パッシブ型チューンドマスダンパーが設置されました。塔は揺れに敏感なエレベータ設備を構築するための試験塔として使用されるため、所有者は、穏やかな日に塔を強制的に振動させる機能を持ちつつ、 疲労の問題を引き起こさないソリューションを探しておられました。強制的な揺れに要求される振幅レベルは、約+/- 200mmの安全な範囲が設定されました。この要件は、ハイブリッドマスダンパー(HMD)または、設計システムは過去に導入された他のHMDシステムとは異なるため、いわゆるデュアルユースTMDを実装するまれな機会を提供しました。このシステムは、パッシブシステムの最適化、アクチュエータのメカニズムの設計、制御アルゴリズム、および安全コンセプトを含め、以下の章で説明します。

5.0 パッシブ型チューンドマスダンパーシステムの最適化
パッシブ型TMDシステムのパラメータは、3つの異なる側面を考慮して特定する必要がありました。つまり、a)追加で十分な構造的減衰機能を提供し、渦励振による動的応答を低減すること、b)パッシブモードで結果として生じるTMD主質量の移動を制限し、横風の突風による励振下にある場合は実現可能/実際的な値とすること、そして c)提供されたアクチュエータによる性能エンベロープを考慮し、励振モードでの望ましい塔の最大変位に必要なエネルギー入力に基づきTMD質量体を選択することです
(つまり、稼働中に発生する最大の力と最大ストローク)。TMDシステムを最適化するために、塔の質量分布、および特定された構造特性で報告されている質量慣性モーメントを表す数値モデルが使用されました。フロア間の剛性要素も、モード形状と実物スケールでの観察からの固有振動数に一致するように調整されました。図6 – 左の図は、採用された類似モデルのモード形状と固有振動数を示しています。図6 – 左の図では、類似モデルのモード形状を、構造コンサルタントが作成した詳細モデルのものと比較しています。


また、TMDは、塔での変位位置もキャプチャする振り子システムとして個別にモデル化されています。支配的な入力ケースの負荷特性、つまり渦励振による共振振動は、単一正弦波振動のそれと非常に類似しています。それでも、共存する風荷重は、本質的に確率的性質のものであり、そのためには、よく知られたDen Hartog条件以外の最適化条件が適用されます。さらに、TMD質量体の相対変位は、調和型荷重よりも確率的荷重に対しての方が大きくなります。最適なTMDパラメータ値の特定には、実際の荷重に近いものを考慮する必要があるため、確率的風荷重(Davenportスペクトルに基づく)と、(渦励振のような)全体的な横風励振に代表される重ね合わせた共鳴コンポーネントの両方を含む時間履歴が生成されました(図7-右を参照)。最適化されたパッシブ型TMDシステムで実現できる塔の変位低減と、その結果生じるTMDの変位を図7-右に示します。
ξ=0.8 %の推定構造減衰に関するこれらの結果に基づき、変位を+/- 650 mm以内に維持しつつ、最適なTMD減衰率を維持し、最高のTMD性能を実現するには、240 tのTMD質量体が必要であることがわかりました。TMD減衰の増加は変位を抑制する可能性があるが、これはアクチュエータの力要件に悪影響を及ぼします。最適化された240 tのTMDセットアップに必要な力を特定するため、類似のモデルを使用して、アクチュエータからの最大力40 kNで、塔の変位が+/- 200mmの範囲となることを確認しました。図7は、類似の数値モデルにおける時間ドメイン数値シミュレーションの結果を示します。このために、結果として生じる塔最上部の変位、TMD質量体の変位、およびそれらを引き起こす有効な力が表示されます。


6.0 制御システムの説明
制御システムの二重性は、a)通常のパッシブモードで発生する振動を低減してエネルギー消費の削減に役立ち、b)共振効果を利用してメインのTMD質量体を励振し、最終的に実際の力の需要を満たすことにより、アクチュエータに求められる力を低減します。したがって、他の制御システム(図10を参照)と比較して、アクチュエータは主要構造物とTMD質量体を接続しますが、典型的なアクティブマスドライバー/ダンパーシステムの場合のようにTMD質量体を直接制御するためには使用されません。
実装されたデュアルユースTMDには、パッシブモード用の240 tの応答質量体が選択されました。励振モードでは、2つのリニアドライブ(各方向に1つずつ)がTMD質量体に取り付けられ、ねじれによるアーチファクトを回避するために、質量体の重心近くにピボットがあります。 各リニアドライブは、+/- 600 mmの最大ストローク内で最大40 kNの力を提供できます(詳細は図9を参照)。リニアドライブは取り外し可能であるため、万が一ベアリングが故障した場合でも、パッシブモード全体がアクチュエータのベアリングの影響を受けることはありません。


図10 – 制御システムのタイプ – パッシブ、セミアクティブ、アクティブ、およびハイブリッドシステムと比較におけるデュアルユースTMD
このシステムには、塔の最上部レベルとTMDの質量加速度を計測するために、4つの加速度計(各方向に1つ)が装備されています。加速度信号は、塔の基本固有振動数(0.1〜0.3 Hz)の範囲内でバンドパスフィルター処理され、塔の速度と変位を特定するために積分されます。
さらに、積分された変位値は、信号のドリフトを比較するために最上部にも設置されている付属のグローバルナビゲーション衛星システムの値と比較できます。初期相関テストは、それに応じて実行されました。加えて、TMDの変位は、リニアモーター内に統合されたストリングポットトランスデューサと誘導長測定システムで直接監視されます。
7.0 制御アルゴリズム
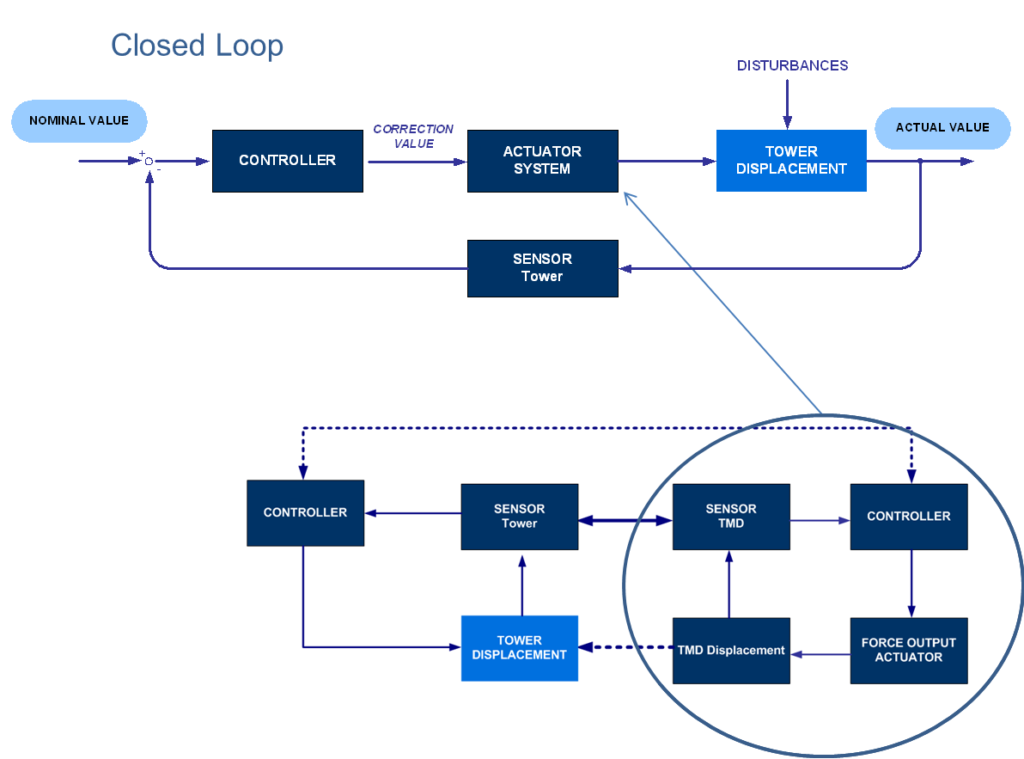
塔の一般的な制御ループは図11にあり、これは、閉ループ制御シーケンスを示しています。制御アルゴリズムの詳細な設計には、アクチュエータとTMD質量体の相互作用に基づく分析モデルが必要で、それにより、アクチュエータ入力と加えられた作用力との間の関係が特定されます。これらは、建物全体の動的挙動を説明する主要構造の分析モデルと組み合わせる必要があります。さらに、 [2]や[3] のように、他のHMDアプリケーションに適用された、または [1] のように理論的に調査された標準制御アルゴリズムと比較して、この塔アプリケーションの制御アルゴリズムでは、1つの主方向の同期制御励振と垂直方向の振動低減を考慮する必要がありました。基本モードで主に動的応答が期待されるため、不安定性を回避するためのすべてのメリットを備えたリニアフィードバック制御をこれらの両方のタスクに適用できます。実際に行われているシンプルな制御として、励振に垂直な塔の動的応答を減衰させるリニアフィードバック制御は、7つの構造動的測定の指定された加重線形合計を通じて該当するアクチュエータを駆動します。これらの測定は、TMDと塔の最上部の加速度、TMDと塔の最上部の速度、TMDと塔の最上部の変位、およびTMDの塔の最上部に対する相対変位に対して行われます。
ここで、事前に選択された重み係数は、単純、正または負のスカラーゲインであることに注意が必要です。重み係数のパラメータ化は、塔の動的試験に基づいており、振動数依存の変更は行われません。アクチュエータの有効なフィードバックは瞬時に(50Hz)計算され、これも以前の動的測定の線形結合となっています。非線形の操作は行われません。制御設計は、アクチュエータ制御における振動低減性能を証明するために、時間ドメインの数値シミュレーション(つまり直接積分)でも実施されました。励振モードでは、同じ制御アプローチが、目的の変位値への塔の励振を表す変位オフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、その他の外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、それに応じて制御値が調整されます。

励振方向に垂直な塔の動的応答を低減するための線形フィードバック制御により、アクチュエータへの力コマンドを、プログラムの7つの動的測定値の指定された加重線形和にできます。これら7つの測定は、TMDと塔の加速度、TMDと塔の速度、TMDと塔の変位、およびTMDの塔に対する相対変位。ここで、重み係数は、単純、正または負のスカラー値であることに注意が必要です。重み係数のパラメータ化は、塔の実験的な動的試験に基づいて行われます。有効なアクチュエータフィードバックは瞬時に(50Hz)に計算され、
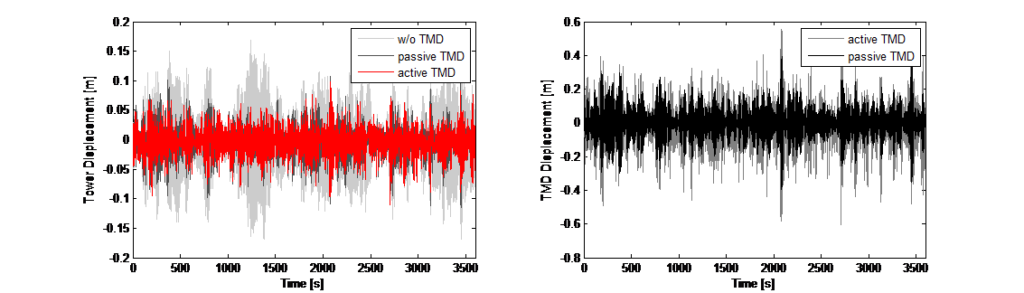
重み係数はスカラー量であり、振動数依存の伝達関数の形式を使用していません。また、フィードバックは動的特性の線形結合です。非線形の操作やロジックはありません。制御設計は、時間ドメインの数値シミュレーション(直接積分)のために実装され、各時間ステップで、アクチュエータ制御としてのTMD質量体への力入力を適合させることができました。図12は、振動抑制のシミュレーションの結果、つまり塔の変位そしてその結果として生じるTMD質量体の変位を示しています。


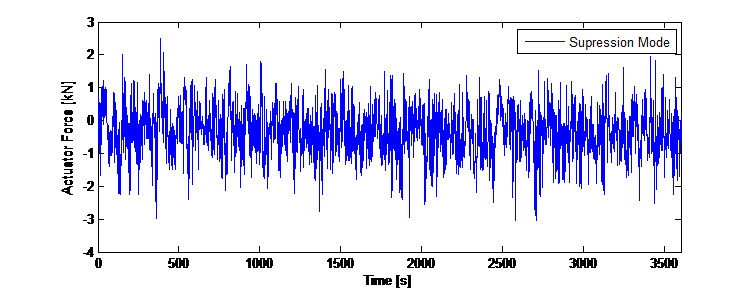
励振モードでは、同じ制御アプローチが、塔の励振を目的の変位値に表すオフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、
それに応じて制御値が調整されます。このオフセットでは、重み係数が実験により特定されました。図13は、単純な正弦波励振と制御アルゴリズムを適用した励振モードでの突風荷重外乱の数値結果を示しています。


8.0 安全性コンセプト
アクチュエータとして使用されるリニアドライブで提供可能な+/- 40 kNの力を考慮し、塔の変位が疲労規定を超えないようにするための安全コンセプトが必ず必要です。これは、力の出力が、所定の+/- 200mmを超える最上部の変位を引き起こすのに十分でない場合にも適用されます。システムの安全性を高めるためのアプローチの1つは、塔の最上部の変位を記録している監視センサーの冗長性を高めることでした。これには、現在の制御ハードウェアとは異なる測定原理を最適に使用する追加の独立した監視システムを実装するのが一番です。ここで紹介されたプロジェクトでは、引用されているように、制御ハードウェアが加速度計、そして構造物の固有振動数の範囲内で信号バンドパスフィルタリングに対して定義された加速度閾値を使用しました。最優先される上位監視システムは、精度が+/- 10 mmのグローバルナビゲーション衛星システム(GNSS)です。
GNNSシステムには、座標データを実際の変位応答値に変換する参照基地局が必要となります。人工励振モード中に塔の最上部変位が所定の閾値を超えると、追加の風やその他の励振が原因となる可能性があり、リレーがアテンダンス信号を0Vに切り替えます。これにより、人工励振モードが中止されます。さらに、両監視システムは、取得したデータに障害のあるセンサー信号がないか常に確認するため、励振モードが有効な場合は中止されます。誤った加速度/ストリングポット信号は、スペクトルピークピッキング条件によって検出されます。該当する範囲でのピークピッキングが可能な場合にのみ、センサーが正しい信号を提供していると見なすことができます。GNNSシステムは、座標データの変化を分析しますが、サンプリングされたデータが時間とともに変化しない場合は、信号における障害が自動的に想定されます。
9.0 振動試験
塔の初期振動試験は、塔がまだ完成していない段階で実施されたため、この段階でのタワーの基本振動数は、パッシブ型TMDシステムが指定した調整範囲を上回っています。TMDは、可能な限り高いチューニング周波数に調整されています。振動試験の目的は、TMDシステムがブロックされた状態で、塔の基本振動数と固有の構造減衰を特定することでした。さらに、パッシブ型TMDシステムを使用した場合の動的挙動と、パッシブ型TMDシステムによる構造的な減衰の増加を特定する必要があります。塔の基本固有振動数を特定するには、平均正規化出力スペクトル密度(ANPSD)法 [1] を利用できます。このためには、記録された時間履歴をセグメントに分割する必要があります。これらのセグメントを周波数ドメインに変換する必要があります。結果として得られるスペクトルは、正規化、平均化し、複素共役スペクトルとの乗算を行う必要があります。
これにより、あらゆるランダムな振動が排除され、構造物で繰り返し発生する自由振動のみが平均化されたスペクトルに表示されます。これは、塔の主に励起された固有振動数を表します。図14の左は、TMDがロックされた状態でのx方向とy方向の水平周囲振動に関して記録された時間履歴を示します。図14の右は、120 秒のセグメント長における平均自動出力スペクトルを示しています。スペクトルは、塔が2つの主要な振動数(x方向に0.225 Hz、y方向に0.245 Hz)で動的応答を示すことを意味しています。
対象の振動モードにおいて周囲の励振が十分な動的応答を引き起こし、確率論的確実を得ると想定している上記の平均出力スペクトル法に加え、固有振動数は、強化型周波数ドメイン分解機能と確率的部分空間同定法を組み込んだ、 [1] 市販の信号処理ソフトウェアARTEMISを使用して特定されました。

強化型周波数ドメイン分解機能(EFDD)と確率的部分空間同定法は、出力のみのモーダルパラメータの特定同定に広く使用されています。


EFDD法は、応答スペクトルの計算に依存します。したがって、スペクトル推定の誤差を低いレベルに保ち、信頼できる方法でモーダルパラメータを抽出するには、長い記録が必要となります。確率的部分空間同定アルゴリズムは、出力のみのモデルを使用してブリッジを特定するために適用されました。確率的部分空間同定法は時間ドメインで機能し、動的問題の状態空間記述に基づいています。異なるモデル次数でのシステム同定結果を比較し、いわゆる安定化図で真の構造モードとスプリアスモードから区別します。これらの図は、特定されたシステムモデルを選択するために広く使用される方法で、真の構造モードが連続するモデル次数に対して安定している傾向があり、自動化された手順で評価される特定の安定化条件を満たしています。図15は、記録された周囲データの安定性カードを示しており、このカードから、該当するモードを特定できます。特定されたモードと、TMDがロックされた状態(左)とTMDが有効な状態(右)での各モードの特定された減衰率も図14に示されています。これにより、構造的な減衰の増加に気付くことができます。構造的な減衰の増加は、調整されていないTMDセットアップが考慮された理論モデルから特定できる理論値の範囲内にあります。
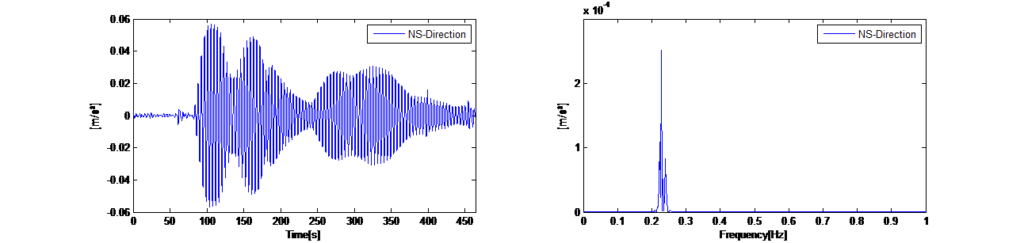
パッシブ型TMDシステムを使用した周囲振動試験に加え、調整されていないTMDシステムの状態にもかかわらず、アクティブ励振モードによる予備テストが行われました。図12の左は、塔の最上部で記録された加速度の時間履歴を示しています。最初の正弦波励振の後、安定した加速レベルのアルゴリズムを有効にして、塔の変位とTMD質量体の強制変位との相関関係を実験で特定しました。図14に示された時間履歴は、励振モードでの2つのテストシナリオを示し、対応するFFTスペクトルは、2つの基本振動数(x方向とy方向)での塔の明確な応答を示しています。 緑でマークされた時間セクションは、アクティブ制御が無効になっている質量体の正弦波励振であり、両方の主方向に動的応答が引き起こされています。結果としてのFFTスペクトルは、2つのピークを示し、これら2つの方向の基本振動数を特定できます。青でマークされた時間セグメントは、アクティブ制御が有効になっている励振用であり、主に一方向でより安定した塔の変位が引き起こされています。励振モードがオフに切り替えられた後に生じる振動の減衰も、構造的減衰を特定するために使用され、D=2.4 %との結果になりました。この結果は、SSIアルゴリズムで特定された減衰率と相関しています。

10.0 結論と展望
デュアルユースTMDは、基本振動数で制御された動的応答に塔を意図的に励振することを目的として、高さ246 mのティッセンクルップ試験塔に設置されています。この励振の目的は、塔の2つの主要な方向に、定義された建物の揺れを引き起こすことです。数値計算に基づき、パッシブモードで必要な減衰により、+/- 200 mmの塔の最上部の変位を実現するために必要な制御力には240 tのTMD質量体が必要であることがわかりました。励振モードの安定した変位レベルを実現し、風と垂直方向の強制振動成分によって引き起こされる変位を抑制するために、制御アルゴリズムが開発され、数値シミュレーションでのテストが行われました。コンクリートスラブを質量体として使用したパッシブ振り子型TMDシステムを設置した後、アクチュエータを稼働させ、初期試験を実施しました。テストにより、塔の固有の構造減衰が予想よりも高いことが明らかになり、関連するすべてのモードを明確に特定できました。建物のアクティブ励振モードは機能しており、建物がまだ完成していないため、すべての動作パラメータを導出するために完全ではないものの、テストは実施できます。建物がまだ完成していない状態であるため、パッシブ型TMDを特定された基本振動数に適合させることはできませんでした。
TMDシステムの適応が完了すれば、すぐにでも引き続きテストを実行できます。これには、振幅依存の減衰と安全コンセプトの完全性に関するテストも含まれます。
参考資料
[1] Wenzel, H., Pichler, D., Schedler, R.(1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.:Mevel, L. (2012).“Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000).“Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003).Passive and active mass damper control of the response of tall buildings to wind gustiness.Eng.Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings.J. Eng.Mech.2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building.Earthq.Eng.Struct.Dyn.2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower.CTBUH J. 2012, 24–29.
[8] Soong, T.T.“Active Structural Control:Theory and Practice”; John Wiley & Sons, Inc.:New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
1.0 会社紹介/ 沿革
エレベーター技術におけるイノベーション用試験施設を収容する目的で、ドイツ南西部に高さ246 mの塔が建てられました。塔は直径20 mの円形のフットプリントの上に建っており、9 つの試験用エレベータシャフト、消防用エレベータ、ガラス製パノラマビューエレベータ用にスペースを提供しています。さらに、試験プログラムを補助する目的で、220 mのシャフトが機械的リフティング用シャフトとして使用されています。
直径40 mの塔の基礎部分にはサービス施設、ロビー、教育センター用の追加スペースが提供されています。232 mのドイツで最も高い展望台からは、晴れた日にはシュヴァルツヴァルト、さらにはアルプスの壮大な景色を眺めることができます。

2.0 構造システム
試験塔の構造システムは、基本的に直径20.8 mの鉄筋コンクリート管となっており、30 mの深さまで周囲の土によって支えられています(図2を参照)。管の厚さは110 mの高さまでは40 cm、それ以上は25 cmとなっています。コイパー層とその下のシェル石灰石からなる土壌は、高い支持力を提供しているため、杭基礎は必要ありませんでした。周囲の土によるクランプ効果に加え、塔の基礎のより広い構造が、より高い横方向の剛性を提供します。
コンクリート管内部の剛性は、主にエレベータシャフトの内壁によるものです。エレベーターシャフトへは、天井スラブが事前に設置されている特定の高さレベルでのみアクセスできます。エレベーターシャフトのいくつかは115 mの高さまでとなっており、鋳造された厚さ40 cmの長いフロアで所定の位置に固定されています。これらのフロアはオフィススペースとして使用されます。高さ197 mまでのボイドスペースの上は、蓄熱およびTMDシステムに使用されます。塔の最上部は、オフィススペースと残りのエレベーターシャフトに使用されます。試験塔の特徴としては、PTFEコーティングを施したガラスファイバーメッシュによるテキスタイルファサードです。メッシュの開口幅は、建物の高さとともに増加し、ファサードは徐々に半透明性が高くなり、材料の密度と重量を低減し、空力効果を向上させています。

ファサードのらせん形状は、スクルートンらせんとして機能することを想定しており、ファブリック自体がコンクリート構造に陰を提供し、直射日光の熱による応力発生を回避するのに役立ちます。ファサードの設計、そして設置における材料面の選択については、メンテナンス性と耐久性、および風荷重を考慮する必要がありました。
3.0 建設工法

試験塔の建設は、以下の手順で行われました。
- 塔の基礎用として30 mの円形建設ピットの掘削。掘削と成形は、まず爆破によって行われました。掘削後、ピットはグラウンドアンカーとコンクリートの吹き付けによって固定されました。
- いかだ基礎の注入
- スリップフォーミングを使用した垂直方向のコンクリート構造物の建設。すべての壁には、4か月間継続して建設が行われました
- フロアスラブの建設
- エントランスエリアの建設
4.0 風荷重に対して予測される動的応答
試験塔の基本振動数は、建設段階とコンクリートの状態(ひび割れ/ひび割れなし)に応じて、0.17 Hz 〜 0.20 Hzの範囲であると予測されました。図4を参照

風解析より、構造物の渦励振は、風速15.3〜16.7 m/s(高さ10m)の範囲において発生しうることが明らかになりました。減衰機能の追加がなければ、この渦励振は上部構造で約+/- 750 mmの振動を引き起こし、内部の職員に不快感を与えるだけでなく、塔のコンクリート構造に重大な疲労寿命への影響を引き起こすと予想されました(図5を参照)。横風による渦励振に対する動的応答を低減するため、パッシブ型チューンドマスダンパーが設置されました。塔は揺れに敏感なエレベータ設備を構築するための試験塔として使用されるため、所有者は、穏やかな日に塔を強制的に振動させる機能を持ちつつ、 疲労の問題を引き起こさないソリューションを探しておられました。強制的な揺れに要求される振幅レベルは、約+/- 200mmの安全な範囲が設定されました。この要件は、ハイブリッドマスダンパー(HMD)または、設計システムは過去に導入された他のHMDシステムとは異なるため、いわゆるデュアルユースTMDを実装するまれな機会を提供しました。このシステムは、パッシブシステムの最適化、アクチュエータのメカニズムの設計、制御アルゴリズム、および安全コンセプトを含め、以下の章で説明します。

5.0 パッシブ型チューンドマスダンパーシステムの最適化
パッシブ型TMDシステムのパラメータは、3つの異なる側面を考慮して特定する必要がありました。つまり、a)追加で十分な構造的減衰機能を提供し、渦励振による動的応答を低減すること、b)パッシブモードで結果として生じるTMD主質量の移動を制限し、横風の突風による励振下にある場合は実現可能/実際的な値とすること、そして c)提供されたアクチュエータによる性能エンベロープを考慮し、励振モードでの望ましい塔の最大変位に必要なエネルギー入力に基づきTMD質量体を選択することです
(つまり、稼働中に発生する最大の力と最大ストローク)。TMDシステムを最適化するために、塔の質量分布、および特定された構造特性で報告されている質量慣性モーメントを表す数値モデルが使用されました。フロア間の剛性要素も、モード形状と実物スケールでの観察からの固有振動数に一致するように調整されました。図6 – 左の図は、採用された類似モデルのモード形状と固有振動数を示しています。図6 – 左の図では、類似モデルのモード形状を、構造コンサルタントが作成した詳細モデルのものと比較しています。


また、TMDは、塔での変位位置もキャプチャする振り子システムとして個別にモデル化されています。支配的な入力ケースの負荷特性、つまり渦励振による共振振動は、単一正弦波振動のそれと非常に類似しています。それでも、共存する風荷重は、本質的に確率的性質のものであり、そのためには、よく知られたDen Hartog条件以外の最適化条件が適用されます。さらに、TMD質量体の相対変位は、調和型荷重よりも確率的荷重に対しての方が大きくなります。最適なTMDパラメータ値の特定には、実際の荷重に近いものを考慮する必要があるため、確率的風荷重(Davenportスペクトルに基づく)と、(渦励振のような)全体的な横風励振に代表される重ね合わせた共鳴コンポーネントの両方を含む時間履歴が生成されました(図7-右を参照)。最適化されたパッシブ型TMDシステムで実現できる塔の変位低減と、その結果生じるTMDの変位を図7-右に示します。
ξ=0.8 %の推定構造減衰に関するこれらの結果に基づき、変位を+/- 650 mm以内に維持しつつ、最適なTMD減衰率を維持し、最高のTMD性能を実現するには、240 tのTMD質量体が必要であることがわかりました。TMD減衰の増加は変位を抑制する可能性があるが、これはアクチュエータの力要件に悪影響を及ぼします。最適化された240 tのTMDセットアップに必要な力を特定するため、類似のモデルを使用して、アクチュエータからの最大力40 kNで、塔の変位が+/- 200mmの範囲となることを確認しました。図7は、類似の数値モデルにおける時間ドメイン数値シミュレーションの結果を示します。このために、結果として生じる塔最上部の変位、TMD質量体の変位、およびそれらを引き起こす有効な力が表示されます。


6.0 制御システムの説明
制御システムの二重性は、a)通常のパッシブモードで発生する振動を低減してエネルギー消費の削減に役立ち、b)共振効果を利用してメインのTMD質量体を励振し、最終的に実際の力の需要を満たすことにより、アクチュエータに求められる力を低減します。したがって、他の制御システム(図10を参照)と比較して、アクチュエータは主要構造物とTMD質量体を接続しますが、典型的なアクティブマスドライバー/ダンパーシステムの場合のようにTMD質量体を直接制御するためには使用されません。
実装されたデュアルユースTMDには、パッシブモード用の240 tの応答質量体が選択されました。励振モードでは、2つのリニアドライブ(各方向に1つずつ)がTMD質量体に取り付けられ、ねじれによるアーチファクトを回避するために、質量体の重心近くにピボットがあります。 各リニアドライブは、+/- 600 mmの最大ストローク内で最大40 kNの力を提供できます(詳細は図9を参照)。リニアドライブは取り外し可能であるため、万が一ベアリングが故障した場合でも、パッシブモード全体がアクチュエータのベアリングの影響を受けることはありません。


このシステムには、塔の最上部レベルとTMDの質量加速度を計測するために、4つの加速度計(各方向に1つ)が装備されています。加速度信号は、塔の基本固有振動数(0.1〜0.3 Hz)の範囲内でバンドパスフィルター処理され、塔の速度と変位を特定するために積分されます。
さらに、積分された変位値は、信号のドリフトを比較するために最上部にも設置されている付属のグローバルナビゲーション衛星システムの値と比較できます。初期相関テストは、それに応じて実行されました。加えて、TMDの変位は、リニアモーター内に統合されたストリングポットトランスデューサと誘導長測定システムで直接監視されます。
7.0 制御アルゴリズム
塔の一般的な制御ループは図11にあり、これは、閉ループ制御シーケンスを示しています。制御アルゴリズムの詳細な設計には、アクチュエータとTMD質量体の相互作用に基づく分析モデルが必要で、それにより、アクチュエータ入力と加えられた作用力との間の関係が特定されます。これらは、建物全体の動的挙動を説明する主要構造の分析モデルと組み合わせる必要があります。さらに、 [2]や[3] のように、他のHMDアプリケーションに適用された、または [1] のように理論的に調査された標準制御アルゴリズムと比較して、この塔アプリケーションの制御アルゴリズムでは、1つの主方向の同期制御励振と垂直方向の振動低減を考慮する必要がありました。基本モードで主に動的応答が期待されるため、不安定性を回避するためのすべてのメリットを備えたリニアフィードバック制御をこれらの両方のタスクに適用できます。実際に行われているシンプルな制御として、励振に垂直な塔の動的応答を減衰させるリニアフィードバック制御は、7つの構造動的測定の指定された加重線形合計を通じて該当するアクチュエータを駆動します。これらの測定は、TMDと塔の最上部の加速度、TMDと塔の最上部の速度、TMDと塔の最上部の変位、およびTMDの塔の最上部に対する相対変位に対して行われます。
ここで、事前に選択された重み係数は、単純、正または負のスカラーゲインであることに注意が必要です。重み係数のパラメータ化は、塔の動的試験に基づいており、振動数依存の変更は行われません。アクチュエータの有効なフィードバックは瞬時に(50Hz)計算され、これも以前の動的測定の線形結合となっています。非線形の操作は行われません。制御設計は、アクチュエータ制御における振動低減性能を証明するために、時間ドメインの数値シミュレーション(つまり直接積分)でも実施されました。励振モードでは、同じ制御アプローチが、目的の変位値への塔の励振を表す変位オフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、その他の外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、それに応じて制御値が調整されます。

励振方向に垂直な塔の動的応答を低減するための線形フィードバック制御により、アクチュエータへの力コマンドを、プログラムの7つの動的測定値の指定された加重線形和にできます。これら7つの測定は、TMDと塔の加速度、TMDと塔の速度、TMDと塔の変位、およびTMDの塔に対する相対変位。ここで、重み係数は、単純、正または負のスカラー値であることに注意が必要です。重み係数のパラメータ化は、塔の実験的な動的試験に基づいて行われます。有効なアクチュエータフィードバックは瞬時に(50Hz)に計算され、
重み係数はスカラー量であり、振動数依存の伝達関数の形式を使用していません。また、フィードバックは動的特性の線形結合です。非線形の操作やロジックはありません。制御設計は、時間ドメインの数値シミュレーション(直接積分)のために実装され、各時間ステップで、アクチュエータ制御としてのTMD質量体への力入力を適合させることができました。図12は、振動抑制のシミュレーションの結果、つまり塔の変位そしてその結果として生じるTMD質量体の変位を示しています。


励振モードでは、同じ制御アプローチが、塔の励振を目的の変位値に表すオフセットと組み合わせて使用されています。オフセットは、各方向に検出された基本振動数に基づく正弦関数です。次に、外乱による上部変位の変位を打ち消すための制御出力が正弦波オフセット関数で変調され、
それに応じて制御値が調整されます。このオフセットでは、重み係数が実験により特定されました。図13は、単純な正弦波励振と制御アルゴリズムを適用した励振モードでの突風荷重外乱の数値結果を示しています。


8.0 安全性コンセプト
アクチュエータとして使用されるリニアドライブで提供可能な+/- 40 kNの力を考慮し、塔の変位が疲労規定を超えないようにするための安全コンセプトが必ず必要です。これは、力の出力が、所定の+/- 200mmを超える最上部の変位を引き起こすのに十分でない場合にも適用されます。システムの安全性を高めるためのアプローチの1つは、塔の最上部の変位を記録している監視センサーの冗長性を高めることでした。これには、現在の制御ハードウェアとは異なる測定原理を最適に使用する追加の独立した監視システムを実装するのが一番です。ここで紹介されたプロジェクトでは、引用されているように、制御ハードウェアが加速度計、そして構造物の固有振動数の範囲内で信号バンドパスフィルタリングに対して定義された加速度閾値を使用しました。最優先される上位監視システムは、精度が+/- 10 mmのグローバルナビゲーション衛星システム(GNSS)です。
GNNSシステムには、座標データを実際の変位応答値に変換する参照基地局が必要となります。人工励振モード中に塔の最上部変位が所定の閾値を超えると、追加の風やその他の励振が原因となる可能性があり、リレーがアテンダンス信号を0Vに切り替えます。これにより、人工励振モードが中止されます。さらに、両監視システムは、取得したデータに障害のあるセンサー信号がないか常に確認するため、励振モードが有効な場合は中止されます。誤った加速度/ストリングポット信号は、スペクトルピークピッキング条件によって検出されます。該当する範囲でのピークピッキングが可能な場合にのみ、センサーが正しい信号を提供していると見なすことができます。GNNSシステムは、座標データの変化を分析しますが、サンプリングされたデータが時間とともに変化しない場合は、信号における障害が自動的に想定されます。
9.0 振動試験
塔の初期振動試験は、塔がまだ完成していない段階で実施されたため、この段階でのタワーの基本振動数は、パッシブ型TMDシステムが指定した調整範囲を上回っています。TMDは、可能な限り高いチューニング周波数に調整されています。振動試験の目的は、TMDシステムがブロックされた状態で、塔の基本振動数と固有の構造減衰を特定することでした。さらに、パッシブ型TMDシステムを使用した場合の動的挙動と、パッシブ型TMDシステムによる構造的な減衰の増加を特定する必要があります。塔の基本固有振動数を特定するには、平均正規化出力スペクトル密度(ANPSD)法 [1] を利用できます。このためには、記録された時間履歴をセグメントに分割する必要があります。これらのセグメントを周波数ドメインに変換する必要があります。結果として得られるスペクトルは、正規化、平均化し、複素共役スペクトルとの乗算を行う必要があります。
これにより、あらゆるランダムな振動が排除され、構造物で繰り返し発生する自由振動のみが平均化されたスペクトルに表示されます。これは、塔の主に励起された固有振動数を表します。図14の左は、TMDがロックされた状態でのx方向とy方向の水平周囲振動に関して記録された時間履歴を示します。図14の右は、120 秒のセグメント長における平均自動出力スペクトルを示しています。スペクトルは、塔が2つの主要な振動数(x方向に0.225 Hz、y方向に0.245 Hz)で動的応答を示すことを意味しています。
対象の振動モードにおいて周囲の励振が十分な動的応答を引き起こし、確率論的確実を得ると想定している上記の平均出力スペクトル法に加え、固有振動数は、強化型周波数ドメイン分解機能と確率的部分空間同定法を組み込んだ、 [1] 市販の信号処理ソフトウェアARTEMISを使用して特定されました。

強化型周波数ドメイン分解機能(EFDD)と確率的部分空間同定法は、出力のみのモーダルパラメータの特定同定に広く使用されています。


EFDD法は、応答スペクトルの計算に依存します。したがって、スペクトル推定の誤差を低いレベルに保ち、信頼できる方法でモーダルパラメータを抽出するには、長い記録が必要となります。確率的部分空間同定アルゴリズムは、出力のみのモデルを使用してブリッジを特定するために適用されました。確率的部分空間同定法は時間ドメインで機能し、動的問題の状態空間記述に基づいています。異なるモデル次数でのシステム同定結果を比較し、いわゆる安定化図で真の構造モードとスプリアスモードから区別します。これらの図は、特定されたシステムモデルを選択するために広く使用される方法で、真の構造モードが連続するモデル次数に対して安定している傾向があり、自動化された手順で評価される特定の安定化条件を満たしています。図15は、記録された周囲データの安定性カードを示しており、このカードから、該当するモードを特定できます。特定されたモードと、TMDがロックされた状態(左)とTMDが有効な状態(右)での各モードの特定された減衰率も図14に示されています。これにより、構造的な減衰の増加に気付くことができます。構造的な減衰の増加は、調整されていないTMDセットアップが考慮された理論モデルから特定できる理論値の範囲内にあります。
パッシブ型TMDシステムを使用した周囲振動試験に加え、調整されていないTMDシステムの状態にもかかわらず、アクティブ励振モードによる予備テストが行われました。図12の左は、塔の最上部で記録された加速度の時間履歴を示しています。最初の正弦波励振の後、安定した加速レベルのアルゴリズムを有効にして、塔の変位とTMD質量体の強制変位との相関関係を実験で特定しました。図14に示された時間履歴は、励振モードでの2つのテストシナリオを示し、対応するFFTスペクトルは、2つの基本振動数(x方向とy方向)での塔の明確な応答を示しています。 緑でマークされた時間セクションは、アクティブ制御が無効になっている質量体の正弦波励振であり、両方の主方向に動的応答が引き起こされています。結果としてのFFTスペクトルは、2つのピークを示し、これら2つの方向の基本振動数を特定できます。青でマークされた時間セグメントは、アクティブ制御が有効になっている励振用であり、主に一方向でより安定した塔の変位が引き起こされています。励振モードがオフに切り替えられた後に生じる振動の減衰も、構造的減衰を特定するために使用され、D=2.4 %との結果になりました。この結果は、SSIアルゴリズムで特定された減衰率と相関しています。

10.0 結論と展望
デュアルユースTMDは、基本振動数で制御された動的応答に塔を意図的に励振することを目的として、高さ246 mのティッセンクルップ試験塔に設置されています。この励振の目的は、塔の2つの主要な方向に、定義された建物の揺れを引き起こすことです。数値計算に基づき、パッシブモードで必要な減衰により、+/- 200 mmの塔の最上部の変位を実現するために必要な制御力には240 tのTMD質量体が必要であることがわかりました。励振モードの安定した変位レベルを実現し、風と垂直方向の強制振動成分によって引き起こされる変位を抑制するために、制御アルゴリズムが開発され、数値シミュレーションでのテストが行われました。コンクリートスラブを質量体として使用したパッシブ振り子型TMDシステムを設置した後、アクチュエータを稼働させ、初期試験を実施しました。テストにより、塔の固有の構造減衰が予想よりも高いことが明らかになり、関連するすべてのモードを明確に特定できました。建物のアクティブ励振モードは機能しており、建物がまだ完成していないため、すべての動作パラメータを導出するために完全ではないものの、テストは実施できます。建物がまだ完成していない状態であるため、パッシブ型TMDを特定された基本振動数に適合させることはできませんでした。
TMDシステムの適応が完了すれば、すぐにでも引き続きテストを実行できます。これには、振幅依存の減衰と安全コンセプトの完全性に関するテストも含まれます。
参考資料
[1] Wenzel, H., Pichler, D., Schedler, R.(1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.:Mevel, L. (2012).“Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000).“Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003).Passive and active mass damper control of the response of tall buildings to wind gustiness.Eng.Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings.J. Eng.Mech.2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building.Earthq.Eng.Struct.Dyn.2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower.CTBUH J. 2012, 24–29.
[8] Soong, T.T.“Active Structural Control:Theory and Practice”; John Wiley & Sons, Inc.:New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
その他の情報源
このトピックに関する詳細な情報が必要ですか?
ご不明な点は、お気軽にお問い合わせください。
当社のプロジェクトエンジニアがまもなくご連絡させていただきます。
その他の情報源
このトピックに関する詳細な情報が必要ですか?
ご不明な点は、お気軽にお問い合わせください。
当社のプロジェクトエンジニアがまもなくご連絡させていただきます。